Elektrischer Schwingkreis
Das geogebra-Applet simuliert eine Reihenschaltung aus einem Ohmschen Widerstand \(R\), einer Induktivität (z.B. Spule) \(L\) und einem Kondensator mit Kapazität \(C\):
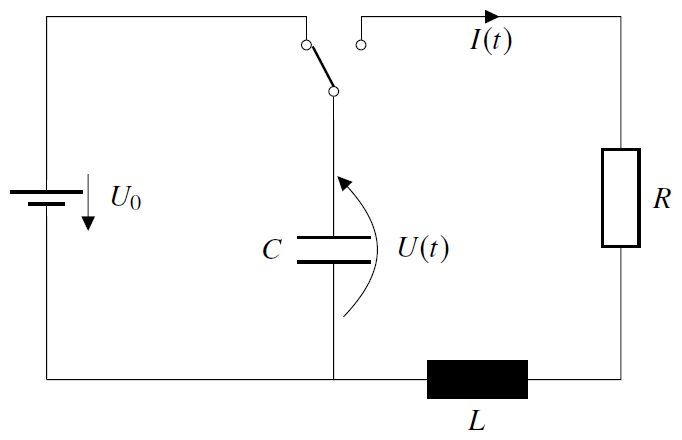
Nachdem man den Kondensator über den linken Stromkreis mit der Gleichspannung (Batterie) \(U_0\) und dem Widerstand \(R_0\) aufgeladen hat, wird der Schalter umgelegt. Der Kondensator entlädt sich, wobei die Stromänderung in der Spule eine Gegenspannung induziert. Diese führt dann zu einem erneuten Aufladen des Kondensators in Gegenrichtung. Anschließend entlädt sich der Kondensator wieder, lädt sich wieder auf usw. Man erhält schließlich sowohl für die Spannung \(U(t)\) als auch für den Strom \(I(t)\) eine gedämpfte Schwingung, weshalb der rechte Stromkreis auch "elektrischer Schwingkreis" genannt wird. Dieser
Schwingfall tritt allerdings nur dann ein, wenn der Widerstand nicht zu groß ist:
$$
R < 2\sqrt{\frac{L}{C}}
$$
Falls der Widerstand diese Grenze überschreitet, fallen Spannung und Strom ohne Schwingung exponentiell ab (Kriechfall).
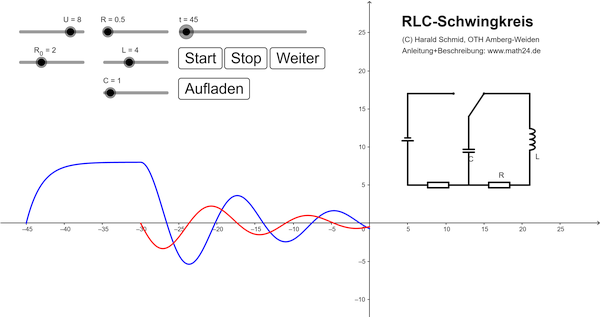
(bitte anklicken)
Anleitung: Mit dem Button "Aufladen" wird der Kondensator mit der Kapazität \(C\) über die Spannungsquelle (z.B. Batterie) aufgeladen. Die Kondensatorspannung steigt rasch bis (fast) zur Batteriespannung \(U_0\) an. Nach dem Umlegen des Schalters mit dem Button "Entladen" wird die Spannungskurve (blau) und die Stromkurve (rot) im Schwingkreis aufgezeichnet. Die Kennwerte aller Bauteile lassen sich durch Schieber verändern. Das sind
- Gleichspannung \(U_0\) und Widerstand \(R_0\) im Ladestromkreis rechts, sowie
- Widerstand \(R\), Induktivität \(L\) und Kapazität \(C\) im Schwingkreis links.
Beschreibung: siehe Buch "Mathematik für Ingenieurwissenschaften: Vertiefung", Kapitel 6, Abschnitt 6.1
 Anschauliche Mathematik für Ingenieure
Anschauliche Mathematik für Ingenieure
