 Anschauliche Mathematik für Ingenieure
Anschauliche Mathematik für IngenieureSimulationen & Visualisierungen
An einer "Bedienstation" (z.B. Montageplatz, Kommissionierbahnhof, Kasse, Ampel, ...) kommen Aufträge mit einer durchschnittlichen Rate \(\lambda\) an, z.B. im Schnitt 1,6 Aufträge pro Minute, und sie werden nach dem FIFO-Prinzip (first in - first out) von einem Bediener mit einer Rate \(\mu\geq\lambda\), z.B. durchschnittlich 2 Aufträge pro Minute, verarbeitet. Für die Ankünfte und für die Bedienung wird jeweils ein "gedächtnisloser" Poisson-Prozess zugrunde gelegt (M = memoryless), und das bedeutet: In einer kurzen Zeitspanne kommt höchstens ein Auftrag an, wobei die verschiedenen Aufträge nichts voneinander wissen. Der Wartebereich soll theoretisch unendlich groß sein, ist hier aber auf 25 Pufferplätze begrenzt. Das Balkendiagramm links zeigt, mit welcher relativen Häufigkeit eine gewisse Anzahl Aufträge im System bis zum simulierten Zeitpunkt anzutreffen war.
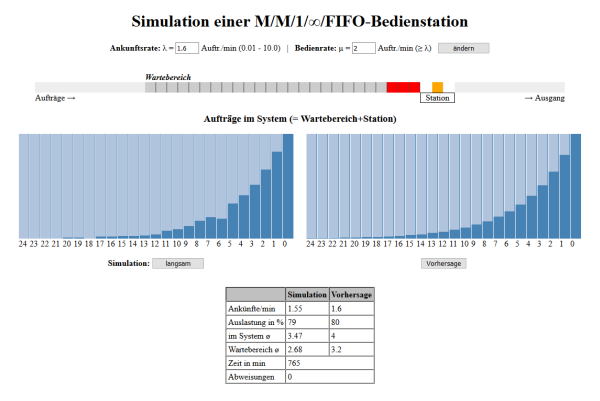
Anleitung: Die Ankunftsrate \(\lambda\) sowie die Bedienrate \(\mu\) werden mit dem Button "ändern" übernommen. Die Simulation startet anschließend automatisch, wobei der Ablauf mit dem Button "schnell" beschleunigt werden kann. Der Button "Vorhersage" berechnet dann anhand der eingegebenen Werte mit Hilfe der Ergebnisse aus der Bedientheorie (bzw. "Warteschlangentheorie") auf der rechten Seite eine Verteilung der Warteschlangenlängen sowie die durchschnittliche Anzahl Aufträge im System.
Beschreibung: siehe Buch "Mathematik für Ingenieurwissenschaften: Vertiefung", Kapitel 7, Abschnitt 7.3.3