 Anschauliche Mathematik für Ingenieure
Anschauliche Mathematik für IngenieureSimulationen & Visualisierungen
Die erste Simulation zeigt die Schwingung zweier Körper \(m_1\) und \(m_2\) mit gleicher Masse \(m\), welche durch Federn mit den Federkonstanten \(D\) (außen) und \(C\) (innen) aneinandergekoppelt sind. Es werden nur die horizontalen Auslenkungen der Massen simuliert - eine vertikale Auslenkung durch die Schwerkraft wird vernachlässigt.
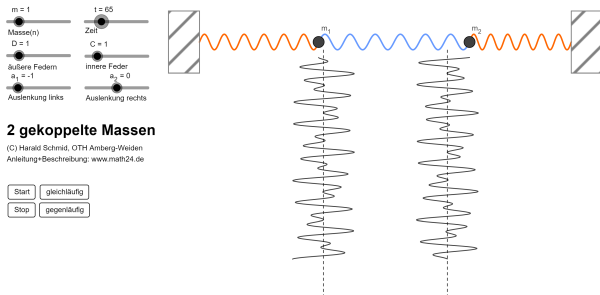
Anleitung: Die Masse \(m\), die Federkonstanten sowie die Auslenkungen \(a_1\) und \(a_2\) der Körper zu Beginn (Zeitpunkt \(t=0\)) der Simulation können durch Schieber verändert werden. Sind die Anfangsauslenkungen \(|a_1|=|a_2|\) betraglich gleich, dann führen die Massen harmonische Schwingungen (= Eigenschwingungen) aus, und zwar im Fall
Beschreibung: siehe Buch "Mathematik für Ingenieurwissenschaften: Vertiefung", Kapitel 6, Abschnitt 6.1
Diese Simulation beschreibt die Schwingung von drei Körpern \(m_1\), \(m_2\), \(m_3\) mit gleicher Masse \(m\), welche durch Federn mit gleicher Federkonstante \(D\) verbunden sind. Es werden nur die horizontalen Auslenkungen berücksichtigt, d.h., die Schwerkraft wird vernachlässigt.
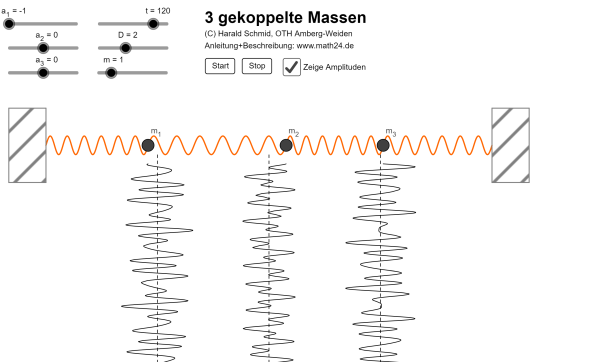
Anleitung: Die Masse \(m\), die Federkonstante \(D\) sowie die Auslenkungen \(a_1\) bis \(a_3\) der Körper am Anfang der Simulation (Zeitpunkt \(t=0\)) können durch Schieber voreingestellt werden. Die zeitliche Entwicklung der Auslenkungen (Amplituden) lässt sich mit dem Kontrollkästchen ein-/ausblenden.