 Anschauliche Mathematik für Ingenieure
Anschauliche Mathematik für IngenieureSimulationen & Visualisierungen
Dieses geogebra-Applet berechnet mit der Formel von Moivre die \(n\)-ten Wurzeln einer komplexen Zahl \(z\) und stellt sie als Zeiger in der Gaußschen Zahlenebene dar. Die \(n\) Wurzelwerte bilden zusammen ein regelmäßiges \(n\)-Eck.
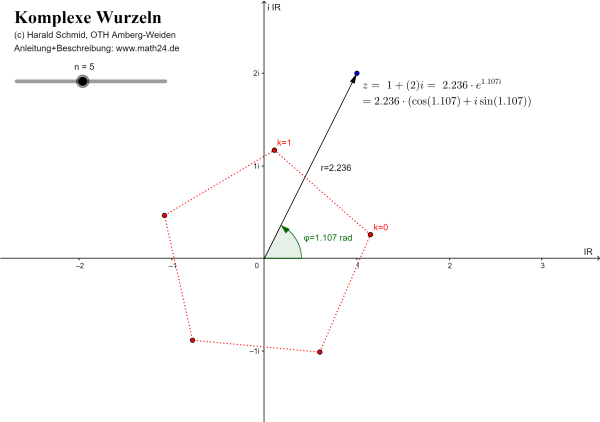
Anleitung: Die komplexe Zahl \(z\) kann direkt durch Verschieben des blauen Punktes in der Gaußschen Zahlenebene festgelegt werden. Zugleich werden neben dem Zeiger die kartesische Form, die Exponentialform und die Polarform von \(z\) angegeben. Dargestellt werden die \(n\) Punkte \(\sqrt[n]{z}\), wobei \(n\) über den Schieber verändert werden kann: \(n=1\) ergibt die Zahl selbst, \(n=2\) die zwei Quadratwurzeln, \(n=3\) die drei Kubikwurzeln usw.
Beschreibung: siehe Buch "Mathematik für Ingenieurwissenschaften: Grundlagen", Kapitel 5, Abschnitt 5.2.5