 Anschauliche Mathematik für Ingenieure
Anschauliche Mathematik für IngenieureSimulationen & Visualisierungen
Auf ein (gedämpftes) Feder-Masse-System mit der Federkonstanten \(D>0\) und dem Reibungskoeffizienten \(R\geq 0\) wirke eine äußere, zeitabhängige Kraft \(F_a(t)\) ein. Die Kräftebilanz (Newton-Axiom & Hooksches Gesetz) ergibt für die Auslenkung \(y(t)\) eine lineare Differentialgleichung 2. Ordnung $$ m\,y'' = -R\,y' - D\,y + F_a(t) $$ mit konstanten Koeffizienten. Falls die äußere Kraft aus einer periodischen Anregung $$ \tfrac{1}{m}\,F_a(t) = F\cdot\sin \Omega\,t $$ mit der Kreisfrequenz \(\Omega>0\) und der Amplitude \(F>0\) resultiert, dann hat die DGl die Form $$ y'' + \tfrac{R}{m}\,y' + \tfrac{D}{m}\,y = F\sin\Omega\,t $$ Das nachfolgende geogebra-Applet simuliert ein solches Federpendel für verschiedene Werte \(m,\,D,\,R,\,F,\,\Omega\):
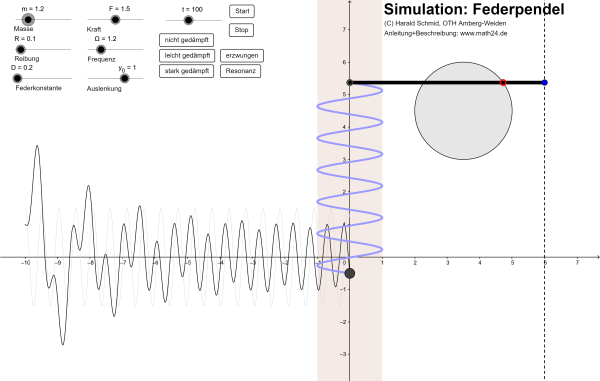
Anleitung: Über die entsprechenden Schieber können die Masse \(m\), die Federkonstante \(D\) und der Reibungskoeffizient \(R\) der Feder sowie die Amplitude \(F\) und die Kreisfrequenz \(\Omega\) der äußeren Kraft eingestellt werden. Darüber hinaus lässt sich die Anfangsauslenkung \(y_0\) der Feder festlegen. Mit den Buttons "Stop" und "Start" wird die Simulation angehalten bzw. fortgesetzt. Über die restlichen Buttons können verschiedene Sonderfälle studiert werden, und das sind:
Beschreibung: siehe Buch "Mathematik für Ingenieurwissenschaften: Vertiefung", Kapitel 3, Abschnitt 3.6.2 - 3.6.3