 Anschauliche Mathematik für Ingenieure
Anschauliche Mathematik für IngenieureSimulationen & Visualisierungen
Ein Planimeter ist ein mathematisches Instrument, welches den Flächeninhalt eines (auch krummlinig begrenzten) Flächenstücks allein durch Umfahren der Randkurve bestimmen kann. Damit lassen sich z.B. Flächen in einer Landkarte oder in einer technischen Zeichnung ermitteln. Dieses geogebra-Applet simuliert die Funktionsweise eines Polarplanimeters, bestehend aus dem Pol im Ursprung, dem Polarm und dem Fahrarm (beide mit gleicher Länge \(a\)), an dessen Ende die Fahrlupe angebracht ist. Nach dem vollständigen Umfahren einer Kurve mit der Fahrlupe (= blauer Ring) im Gegenuhrzeigersinn kann man den Inhalt der eingeschlossenen Fläche am Messrad ablesen.
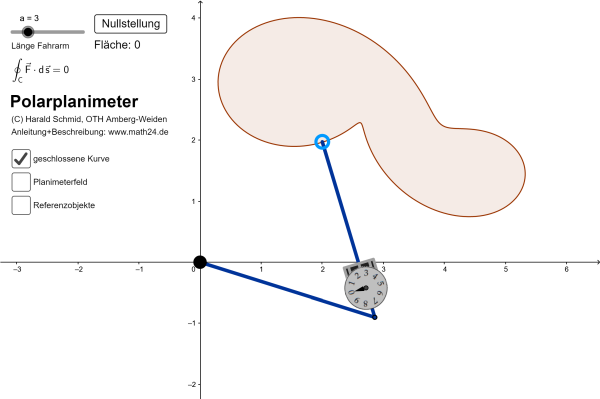
Anleitung: Zu Beginn sollte man das Messrad auf 0 stellen. Als Testobjekte sind ein Quadrat mit Fläche 1 und ein Kreis mit Fläche \(\pi\) vorhanden. Beide können über das Kontrollkästchen "Referenzobjekte" angezeigt werden. Die Länge des Pol-/Fahrarms \(a\) lässt sich mit dem Schieber verändern. Das Messrad registriert dann den Wert $$A = a\oint_C \vec F(\vec r)\cdot d\vec r$$ Hierbei ist \(\vec F=\vec F(\vec r)\) ein Vektorfeld, das "Planimeterfeld", welches vom Startwert bis zu einem Punkt auf der umfahrenen Kurve \(C\) integriert wird. Das Planimeterfeld kann durch das gleichnamige Kontrollkästchen eingeblendet werden. Im Fall einer geschlossenen Kurve entspricht \(A\) dem Inhalt der umfahrenen Fläche, wie man z.B. mit dem Integralsatz von Green zeigen kann.
Beschreibung: siehe Buch "Mathematik für Ingenieurwissenschaften: Vertiefung", Kapitel 5, Abschnitt 5.1.3.4