 Anschauliche Mathematik für Ingenieure
Anschauliche Mathematik für IngenieureSimulationen & Visualisierungen
Wie stellt ein Computer mit einer möglichst einfachen Rechnung fest, ob ein Punkt \(P\) innerhalb oder außerhalb eines vorgegebenen Vierecks liegt? Es gibt eine Möglichkeit, dies allein mit Grundrechenarten zu prüfen! Dazu bezeichnen wir die Ecken des Vierecks, die im Gegenuhrzeigersinn durchlaufen werden, mit \(ABCD\) und betrachten zunächst die Vektoren $$\vec v_A := \overrightarrow{AB}\quad\mbox{und}\quad\vec p_A := \overrightarrow{AP}$$ von \(A\) nach \(B\) bzw. von \(A\) zum Punkt \(P\). Der um 90° im Uhrzeigersinn gedrehte Vektor \(\vec n_A\) zu \(\vec v_A\) steht dann senkrecht auf der Seite \(AB\) und zeigt in Richtung des Inneren von \(ABCD\). Das Skalarprodukt \(\vec n_A\cdot\vec p_A = |\vec n_A|\cdot|\vec p_A|\cdot\cos\sphericalangle(\vec n_A,\vec p)\) ist also genau dann positiv, wenn der Winkel \(\sphericalangle(\vec n_A,\vec p)\) zwischen \(\vec n_A\) und \(\vec p_A\) betragsmäßig kleiner ist als 90°, was wiederum bedeutet, dass \(P\) auf der linken Seite von \(\vec v_A\) liegt. Gilt dagegen \(\vec n_A\cdot\vec p_A < 0\), dann liegt der Punkt rechts von der Seite \(AB\), und im Fall \(\vec n_A\cdot\vec p_A = 0\) liegt er auf der Geraden durch \(A\) und \(B\). Diese Überlegung lässt sich auf die anderen drei Seiten \(BC\), \(CD\), \(DA\) übertragen. Der Punkt \(P\) liegt demnach genau dann im Inneren des Vierecks \(ABCD\), wenn alle vier Skalarprodukte positiv sind. Die Skalarprodukte wiederum kann der PC allein mit den vier Grundrechenarten ausrechnen...
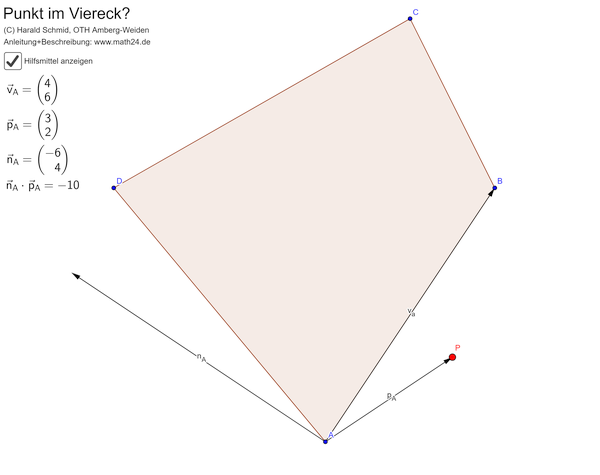
Anleitung: Verschieben Sie den Punkt \(P\) mit der Maus! Sobald er im Inneren des Vierecks liegt, wechselt seine Farbe von rot auf grün. Die Punkte des Vierecks können ebenfalls verschoben werden. Nach Aktivierung des Kontrollkästchens "Hilfsmittel anzeigen" ist die vom PC durchgeführte Berechnung des Skalarprodukts am Beispiel der Seite \(AB\) zu sehen: Allein das Vorzeichen von \(\vec n_A\cdot\vec p_A < 0\) entscheidet, ob sich \(P\) links oder rechts von \(AB\) befindet.
Beschreibung: siehe Buch "Mathematik für Ingenieurwissenschaften: Grundlagen", Kapitel 3, Abschnitt 3.1.2