 Anschauliche Mathematik für Ingenieure
Anschauliche Mathematik für IngenieureSimulationen & Visualisierungen
Das geogebra-Applet veranschaulicht die komplexen Funktionswerte eines Polynoms 4. Grades $$P(z)=z^4 + a_3 z^3 + a_2 z^2 + a_1 z + a_0$$ Genauer: Es werden die Polynomwerte für eine komplexe Variable \(z=r\,e^{i\varphi}\) mit einem festen, aber frei einstellbaren Betrag \(r\) berechnet und mit dem Faktor \(s=1/(r^n+1)\) skaliert, damit die Funktionswerte betragsmäßig nicht zu groß werden. Die Punkte \(s\cdot P(r\,e^{i\varphi})\) erzeugen für \(\varphi\in[-\pi,\pi]\) eine geschlossene Kurve in der Gaußschen Zahlenebene. Die Zahl \(z\) ist genau dann eine komplexe Nullstelle des Polynoms, falls die Kurve \(s\cdot P(z)\) durch den Ursprung \(0\) verläuft.
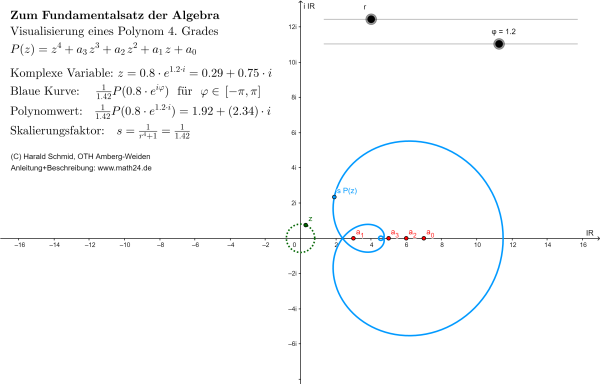
Anleitung: Der Betrag \(r\) lässt sich mit dem Schieber rechts oben einstellen, während die komplexen Koeffizienten \(a_0,...,a_4\) des Polynoms durch Verschieben der gleichnamigen Punkte in der Gaußschen Zahlenebene verändert werden können. Die blaue Kurve zeigt die Polynomwerte \(s\,P(z)\) für die komplexe Variable \(z=r\,e^{i\varphi}\) mit dem voreingestellten Betrag \(r\) bei einem vollen Umlauf des Arguments \(\varphi\in[-\pi,\pi]\) an. Mit dem Schieber für \(\varphi\) kann man eine komplexe Zahl \(z\) auswählen. Diese wird auf dem grün gepunkteten Kreis angezeigt, während der Bildpunkt (= Polynomwert) \(s\cdot P(z)\) auf der blauen Kurve erscheint. Bewegt man den Schieber für den Betrag von \(r=0\) bis zum Maximalwert, dann lässt sich eine Veränderung der blauen Kurve beobachten: Sie befindet sich für kleine Beträge \(r\) nahe dem Punkt \(a_0\) außerhalb von \(0\) und nähert sich mit steigendem Betrag immer mehr einem Kreis um den Ursprung mit Radius \(1\) an. Da sich die Kurve in Abhängigkeit von \(r\) stetig verändert und der Punkt \(0\) von außerhalb nach innerhalb der Kurve wandert, muss es einen Wert \(r\) geben, bei dem die blaue Kurve durch den Ursprung \(0\) verläuft. Es gibt demnach auch ein Argument \(\varphi\), bei dem die Zahl \(z=r\,e^{i\varphi}\) den Funktionswert \(s\cdot P(z)=0\) liefert, und dieser Wert \(z\) ist dann eine komplexe Nullstelle des Polynoms \(P(z)\). Mit einer ähnlichen Überlegung kann man zeigen, dass jedes Polynom vom Grad \(n>0\) mindestens eine komplexe Nullstelle haben muss.
Beschreibung: siehe Buch "Mathematik für Ingenieurwissenschaften: Grundlagen", Kapitel 5, Abschnitt 5.7.1